DRIVESIM
解析事例 [ホームへ]−遊星歯車機構
(プラネタリギア方式CVT)HEV車両の駆動力-遊星歯車機構方式の
CVTの走行性能線図(車速―駆動力)を描いてみます。------------------------------------------------------------------------------------------
<理論的考察>
通常パラレルハイブリッド車では現回転数でのエンジンとモータの各々の最大出力を合計した動力を駆動用に出力できますが
プラネタリギア方式の
CVTはこれと異なる出力特性を持ちます。上図でエンジンとモータの最大出力を
Peg, Pmtとします。エンジンを目標回転数に制御するためにはエンジンに負荷をかける必要がありそのためエンジンに発電機を駆動させ発電させます。 これは電機動力計でエンジン動力を計測する際エンジン回転数を制御するのに
動力計の発電電力を制御するのと基本的には同じです。発電機による負荷を
Pgnとするとエンジンが直接車両駆動に供給できる動力はPeg_drive=Peg-Pgn
となります。発電機で発電した電力はそのままモータに供給されるものとし、モータに還流される動力を
Pgn_recirculationとします。還流される動力
Pgn_recirculationがモータの最大出力未満ならバッテリからモータに電力を供給し、逆にモータの最大出力を超えていたら超過分の電力をバッテリに蓄えれば、結果として還流される電力に関係なく常にモータはその最大出力を車両駆動用に
供給できることになります。 以上をまとめるとプラネタリギア方式の
CVTが車両駆動用に出力できる合計動力の最大値はPeg+Pmt-Pgn
ということになります。
<遊星歯車バランス計算式>
遊星歯車における
3軸の回転速度、トルク、および動力のバランス式を用いて最大駆動動力と駆動力を求めます。Suffix
は以下P:
動力 s:サンギア軸(発電機) m:モータT:
トルク c:キャリア軸(エンジン) l:駆動動力ω:回転速度
r:リングギア軸(モータ)N:
歯数α:
Nr/NsV:
車速F:
駆動力●回転速度バランス
ω
s-(1+α)ωc+αωr=0---------------------------------------------(1)●トルクバランス
Ts+2/(1+
α)Tc+1/αTr=0ここでトルク
TはT=P/(2πω)なのでPs/
ωs+2/(1+α)Pc/ωc+1/αPr/ωr=0-------------------------------(2)●エネルギバランス
Ps+Pc+Pr=0
ここでリングギア側の動力はモータ動力
Pmと駆動動力Plの反力(−)の合計であるのでPr=Pm-Pl
よって
Ps+Pc+Pm-Pl=0-----------------------------------------------(3)ω
rは車速から求まり、Pcとωcは車速vsエンジン出力のマップから求まりPmはモータの最大出力から求まる。したがって未知変数は
Ps, ωs, Plの3変数である。(3)
式よりPs=Pl-Pc-Pm---------------------------------------------------(4)
(1)
式よりω
s=(1+α)ωc-αωr----------------------------------------------(5)(4), (5)
式を(2)式に代入し整理するとPl=
{(Pc+Pm)/ωs-2//(1+α)Pc/ωc-1/αPm/ωr}/(1/ωs-1/α/ωr)--------(6)よって駆動力
FはF=Pl/V
但しこれは
Psが発電機最大吸収動力(発電機として駆動するための動力)を超えない条件での計算式。<サンプル計算>
●車両システム
・車重
820kg ・エンジン 55KW ・モータ 50KW ・発電機 25KW・トランスミッション プラネタリギア方式
CVT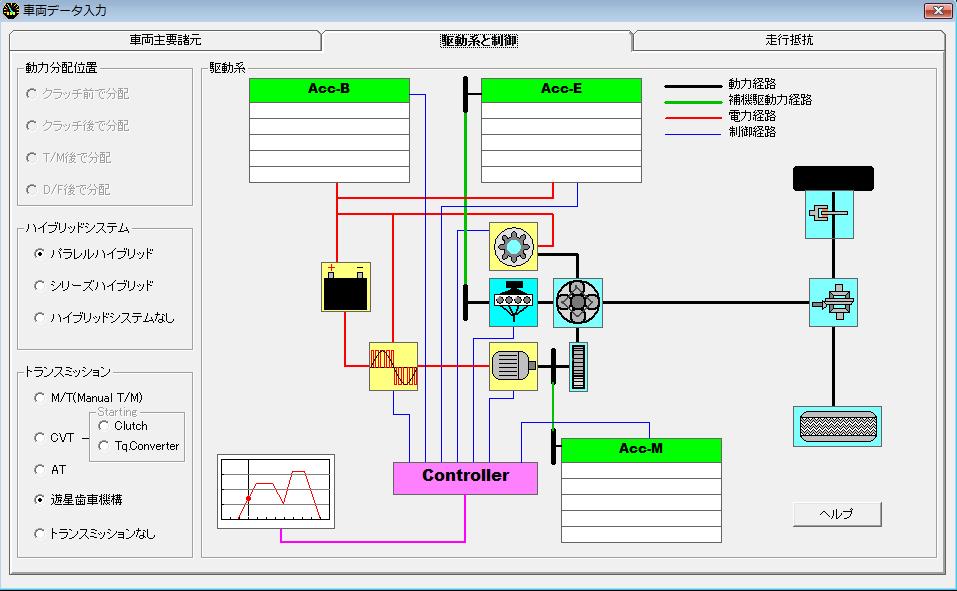
・遊星歯車
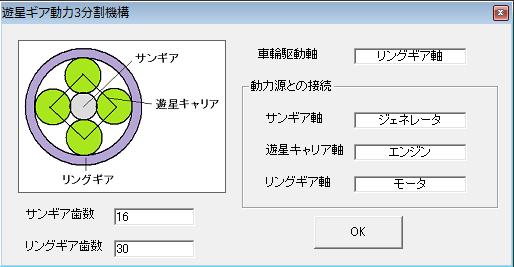
<走行性能線図>