第3回 ねじり振動を伴う回転運動の計算 前へ
一般に機械の回転運動はねじり振動を伴う。
一定負荷の一定速度運転においても何らかのトルク変動・揺らぎが原因でねじり振動が発生する。
特に長い軸や大きな慣性モーメントを持つ回転機械ではねじり共振回転数を避けて運転するよう注意が
必要である。また負荷トルクが変動する機械の駆動など負荷が大きなねじり振動の加振源となる場合は
モータや駆動系に振動を伝達しないよう制振・吸振対策を施す必要がある。
共振・制振問題には周波数応答解析がよく用いられる。これは一定周期の加振力を十分長い時間作用させ
振動が一定状態に収束した状態での振幅や位相など振動の様子を調べるものであり振動の運動方程式を
直接解かなくても振動数解が得られるという利点がある。 しかし加振力の周期が短時間で変化する
「過渡状態」の解析には十分とはいえない。
過渡状態の代表例はモータの始動/停止であり回転速度は停止と定常運転速度の間を短時間で推移する。
負荷トルク変動が大きい機械では、モータ駆動トルクと負荷トルクおよびねじり振動による弾性トルクの
相互作用により振動が大きくなり始動が困難になることがある。このような過渡状態での振動を扱うには
振動の運動方程式を直接解く必要がある。
(1)ねじり弾性軸で連結された複数の回転体の運動

モータやタービンと発電機・コンプレッサなど比較的多く見かけるケースである。
回転体は剛体(ねじり弾性係数が十分大きい)とし軸のみが弾性体であるとする。
実体としての軸は長さを有し、ねじり振動は軸長手方向に往復伝播するので厳密な計算には
軸のねじり運動の方程式を用いる必要がある。しかし
○運転によって加わる加振力の振動数が高々1次共振振動数(基本振動数)程度
○軸の一部が他の軸部にくらべ極端にねじり剛性が弱い(弾性カップリングなど)
などの場合は軸を単純な「ねじりバネ」とみなすことができる。
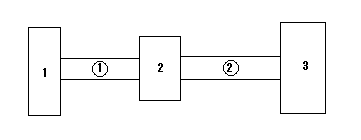
まず回転体2個,弾性軸1本のケースを考える。
モータトルク Tm:回転体-1に作用
回転体-1 の
慣性モーメント I1
回転角 θ1
回転角速度 ω1
負荷トルク Tl1
弾性軸よりモータ側の回転体-2の
慣性モーメント I2
回転角 θ2
回転角速度 ω2
負荷トルク Tl2
弾性軸-1の
弾性係数 E1
粘性減衰係数 C1
弾性軸-1が弾性カップリングの場合E1,C1はカタログ値や実験値を用いる。
弾性軸-1が断面積一定の中空軸の場合,軸の横弾性係数をG、内外径をdi,do,長さをLとすると
E1=π・(do^4-di^4)・G/(32・L)
弾性軸-1のねじれ角は回転体-1,-2の回転角の差(θ1-θ2)でありねじり弾性係数はE1であるので
弾性軸-1の弾性トルクは
E1・(θ1-θ2)
また回転体-1,-2の相対回転角速度は(ω1-ω2)あり減衰係数はC1であるので減衰トルクは
C1・(ω1-ω2)
回転体-1の運動方程式
I1・(dω1/dt)=Tm-Tl1+E1・(θ2-θ1)+ C1・(ω2-ω1)
(dω1/dt)=(Tm-Tl1+E1・(θ2-θ1)+ C1・(ω2-ω1))/ I1
ω1=(dθ1/dt)
同-2
I2・(dω2/dt)=E1・(θ1-θ2)-Tl2+ C1・(ω1-ω2)
(dω2/dt)=(E1・(θ1-θ2)-Tl2+ C1・(ω1-ω2))/ I2
ω2=(dθ2/dt)
以上θ1、θ2、ω1、ω2に関する連立微分方程式を解く.
弾性軸が2本、回転体が3つ以上の場合はさらに回転体毎に運動方程式を追加していく。
i番回転体に作用するトルクはi-1番弾性軸からの弾性トルクをTeli-1、i番弾性軸からの弾性トルクを
Teliおよびi番回転体に作用する負荷トルクをTli とすると
Teli-1= Ei-1・(θi-1-θi)+ Ci-1・(ωi-1-ωi)
Teli= Ei・(θi+1-θi)+ Ci・(ωi+1-ωi)
(dωi/dt)=(Teli-1+Teli-Tli)/ Ii
ωi=(dθi/dt)
過渡状態をあつかう場合はモータトルクTm,負荷トルクTlは速度・回転角・時間などの関数として
できる限り実際に近い値で与える。
例)
モータトルク :T-N性で示されるとおりトルクTは回転速度Nの関数となる
変動のある負荷トルク:一般に変動は回転角の関数となることが多い
上記微分方程式は解析的には解けないのでコンピュータを用いた数値計算が必要になる。
ただRunge-Kutta法など簡単な陽解法で解を求めることができるし、C,Basic,Fortranなどで記述
された数値計算用ソースプログラムも多くの書籍で紹介されているので参照するとよい。
(数値計算の詳細については別の機会に解説する。)
(2)変速軸に弾性カップリングを配した系の運動
モータ軸に直接ではなく変速後の軸に弾性軸(弾性カップリング)が取り付けられている場合は第1回
「エネルギ保存則を用いた動力計算法」の(1)「モータ軸に対し一定速度比で回転する複数の回転軸
からなる駆動系」で解説したモータ軸換算等価慣性モーメントおよびモータ軸換算等価トルクを応用する。
モータで駆動される第1軸からn軸までn本の回転軸を持つシステムでk番軸とk+1番軸間に弾性カップリング
が取り付けられているとする。
動力伝達経路上カップリングよりモータ側の軸群のモータ軸換算等価慣性モーメントおよび等価トルクは
k k
Idv=Σ(Ii・ri2/ηi); Tldv=Σ(Ti・ri/ηi)
1 1
動力伝達経路上カップリングより反モータ側の軸群では
n n
Idn=Σ(Ii・ri2/ηi) Tldn=Σ(Ti・ri/ηi)
k+1 k+1
ただしk,k+1軸はカップリングで連結されているのでrk=rk+1, ηk=ηk+1
k,k+1軸間にある弾性カップリングによる伝達トルクは
Tc=E・(θk-θk+1)+ C・(ωk-ωk+1)
θk,θk+1,ωk,ωk+1 を各々モータ軸に換算した値をθdv,θdn,ωdv,ωdnとすると
θk=rk・θdv θk+1=rk・θdn ωk=rk・ωdv ωk+1=rk・ωdv
Tc=(E・(θdv-θdn)+ C・(ωdv-ωdn))・rk
Tcのモータ軸換算値をTceとすると
Tce=(E・(θdv-θdn)+ C・(ωdv-ωdn))・rk2/ηk
=E・rk2/ηk ・(θdv-θdn)+ C・rk2/ηk・(ωdv-ωdn)
Tce=Ee・(θdv-θdn)+ Ce・(ωdv-ωdn)
Ee= E・rk2/ηk
Ce= C・rk2/ηk
Ee、Ceは各々モータ軸換算弾性係数、モータ軸換算粘性減衰係数である。
以上複数軸をモータ軸に換算した等価値を用いると以下のように(1)と同じ式が使える。
駆動側
Idv・(dωdv/dt)=Tm-Tldv+Ee・(θdn-θdv)+Ce・(ωdn-ωdv)
(dωdv/dt)=(Tm-Tldv+Ee・(θdn-θdv)+Ce・(ωdn-ωdv))/ Idv
ωdv=(dθdv/dt)
被駆動側
Idn・(dωdn/dt)=Ee・(θdv-θdn)-Tldn+ Ce・(ωdv-ωdn)
(dωdn/dt)=(Ee・(θdv-θdn)-Tldn+ Ce・(ωdv-ωdn))/ Idn
ωdvn=(dθdn/dt)
以上θdv、θdn、ωdv、ωdvn に関する連立微分方程式を解く