機械や流体の運動を運動量保存則を用いて記述すると運動方程式から出発するよりはるかに簡単に計算
できることがある。今回は回転軸の運動や流路内流れに運動量保存則を適用する例を解説する。
(1)クラッチによる負荷継合
(1-1)急峻な継合
運転中のモータに電磁クラッチ等を用いて急峻に負荷を継合することがある。
モータ側から見るとクラッチトルクにより回転速度が低下、負荷側から見るとクラッチトルクにより
回転速度が上昇、そして両者の速度が等しくなった時点で継合が完了する。
クラッチ伝達トルクがモータトルクに比べはるかに大きく、継合に要する時間も短い場合にはこの間
モータと負荷の運動変化にはクラッチ伝達トルクのみが関与していると考えてよい。
このようにシステムになんら外力が作用せず構成要素間の力・トルクのみが作用する場合は「運動量保存則」
が成立する。つまり「システムを構成する要素の運動量の合計は一定」である。
モータ側の
慣性モーメントを Im
初期回転角速度を ω
負荷側の
慣性モーメントを Il
初期回転角速度を ωl
負荷継合後の両者の回転角速度を ω
運動量保存則から負荷継合前後のシステムの運動量は等しい
Im・ωm+Il・ωl=(Im+Il)・ω
ω=(Im・ωm+Il・ωl)/(Im+Il)
負荷継合によるモータ回転速度変化は
Δωm=ωm-ω
=(ωm-ωl)・Il/(Im+Il)
次に系のエネルギについて検証する。
負荷継合前の運動エネルギ
モータ側運動エネルギ Km=1/2・Imωm2
負荷側運動エネルギ Kl=1/2・Ilωl2
負荷継合後の運動エネルギ
両者一体の運動エネルギ K=1/2・(Im+Il)・ω2
ここで
ω=(Im・ωm+Il・ωl)/(Im+Il)
K=1/2・(Im・ωm+Ilωl)2/(Im+Il)
したがって継合前後の運動エネルギの差は
ΔK=K-(Km+Kl)
=1/2・Im・ωm+Il・ωl)2/(Im+Il)-1/2・Im・ωm2-1/2・Il・ωl
=-1/2・Im・Il・(ωm-ωl)2/(Im+Il)
ΔKはωm=ωlでない限り負であり、これは負荷継合には必ずエネルギ損失を伴うことを意味する。
実際にはクラッチの摩擦熱エネルギとして放逸する。
以上運動量保存則を用いると簡単に継合後の回転速度やエネルギ損失が求まる。
しかし継合に要する時間を求めたり継合中のモータトルクが無視できない場合には適用できない。
(1-2)ソフトな継合
自動車の発進等でクラッチ面圧(伝達トルク)を制御しながら時間をかけてソフト継合を行う場合は
その間にモータから供給される動力、負荷側の抵抗トルク等が無視できず、しかもそれらは外力なので継合
前後の運動量保存則は使えない。
「系の角運動量の時間変化は外力モーメント(トルク)の和に等しい」という「運動量則」
L=I・ω L:角運動量
(dL/dt)=T T:外部トルク
を用いることもできるがこちらは微分式でありむしろ同じ微分式なら運動方程式から出発する方が
わかりやすい。
モータ側
モータトルク Tm
角速度 ωm
慣性モーメント Im
負荷側
抵抗トルク Tl
角速度 ωl
慣性モーメント Il
クラッチ伝達トルク Tc
モータ側の運動方程式
Im(dωm/dt)=Tm-Tc
(dωm/dt)=(Tm-Tc)/Im
負荷側の運動方程式
Il(dωl/dt)=Tc-Tl
(dωl/dt)=(Tc-Tl)/Il
これらモータ側と負荷側の運動方程式を連立させて求めていくことになる。
ただしクラッチは滑っている場合と継合している場合とで伝達トルクTcが異なる不連続な性質を持つので
通常用いられるRunge-Kutta法などの陽解法で安定した解をえることが難しく数値計算上の工夫が
必要である。
そこで継合期間中Tm,Tc,Tlを一定として次のようにして簡易計算をおこなう。
ωm=ωm0+am・t am=(Tm-Tc)/Im
ωl=ωl0+al・t al=(Tc-Tl)/Il
継合時間t
ωm0+am・t=ωl0+al・t
(am-al)・t=ωl0-ωm0
t=(ωl0-ωm0)/(am-al)
継合後回転速度
ω=ωm0+am・(ωl0-ωm0)/(am-al)
=(am・ωl0-al・ωm0)/(am-al)
(2)慣性モーメントの変化する自由回転運動
モータ駆動系でモータ動力を止め惰行状態で自由回転しながら慣性モーメントが変化する場合の運動を考える。
例えば第1回でものべた垂直軸に対し傾斜したアームを持ち垂直軸周りに回転しながらアームの姿勢変化
や伸縮を行うロボット機構などが相当する。この自由回転運動には外力が作用しないので運動量保存則が
成り立つ。
d(I・ω)=0
I・dω+ω・dI=0
時間tで微分
I・(dω/dt)+ω・(dI/dt)=0
(dω/dt)=-ω/I・(dI/dt)
つまり回転角速度の時間変化は慣性モーメントの時間変化に対し比例関係にあり
慣性モーメントが大きくなる方向に変化すると回転速度は下がる方向に変化する。
さらに初期速度ω0と慣性モーメントI0が与えられている場合、慣性モーメントが変化し
Ixとなった場合の回転速度ωxは
I0・ω0=Ix・ωx
ωx=(I0/Ix)・ω0
運動エネルギの差は
ΔK=1/2・I0・ω02-1/2・Ix・ωx2
角運動量をLとすると
L=I0・ω0=Ix・ωx
ΔK=1/2・L・(ω0-ωx)
このエネルギは慣性モーメントを変えるためにシステム内部から供給される必要がある。
(3)流路に設けられた斜平板にかかる荷重
一般に流体運動には連続式(質量保存)と運動方程式もしくはそれから導かれ別名ベルヌイの式と呼ばれる
エネルギ保存式を用いて計算できる。しかしこれらの式から複雑な労作を経て計算する問題も運動量式を
用いると実に簡単に解決できることがある。

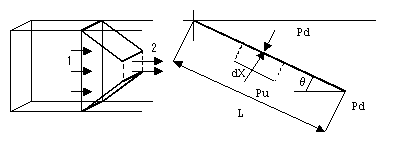
矩形流路にノズルを形成する1対の斜板が設けられている。流体が流れる時に斜板に作用する力を求める。
因みにこれは自動開閉弁(リード弁)のリフトや流量を求める際に必要な計算である。
流路幅 B
斜板長さ L
1における流路断面積 A1
流速 V1
2における流路断面積 A2
流速 V2
Xにおける面積 A
流量 Q
流体密度 ρ
(3-1) 荷重を積算(積分)する方法
斜板に作用する荷重は板の表裏両面に作用する圧力荷重差による。したがって圧力荷重差を斜板前面にわたり
積算すれば荷重が求まる。いま斜板上の微小距離dXをとる。
上流側(板表面)圧力をPu,下流(板背面)圧力をPdとすると
エネルギ式から
1/2・ρ・Vu2+Pu=1/2・ρ・Vd2+Pd
差圧をΔP
ΔP=Pu-Pd=1/2・ρ・(Vd2-Vu2)
Vu=Q/A Vd=Q/A2
dx間に作用する荷重は
ΔP・B・dx=1/2・ρ・(Q/A2)2-(Q/A)2)・dx
=1/2・ρ・Q2・B・(1/A22-1/A2)・dx
斜板全体の荷重Fは
L
F=1/2・ρ・Q2・B・∫(1/A22-1/A2)・dx
0
L L
=1/2・ρ・Q2・B・(∫(1/A22)・dx-∫(1/A2)・dx)
0 0
L
=1/2・ρ・Q2・B・L/A22-∫(1/A2)・dx)
0
A2
=1/2・ρ・Q2・B・(L/A22-∫(1/A2)・dA・(dx/dA))
A1
dx/dA=1/(dA/dx)=1/((A2-A1)/L)=L/(A2-A1)
F=1/2・ρ・Q2・B・(L/A22-(1/A2-1/A1)・ L/(A2-A1))
最後に求める荷重Fは
F=1/2・ρ・Q2・B・L・(A1-A2)/(A1・A22)
(3−2)運動量則を用いる方法
荷重積算で求める方法に代わり運動量則を用いる。
1,2での単位時間あたりの運動量の差は外力に等しい。
1,2間の流体に作用する外力は1,2での圧力および上下1対の斜板からの反力fの流れ
方向成分fxである
運動量則
ρ・Q・(v2-v1)=P1・A1-P2・A2-fx
fx=ρ・Q・(v1-v2)+P1・A1-P2・A2
v1=Q/A1,V2=Q/A2
1/2・ρ・V12+P1=1/2・ρ・V22+P2
P1=P2+1/2・ρ・(v22-v12)=P2+1/2・ρ・((Q/A2)2-(Q/A1)2)
fx=ρ・Q・((Q/A1)-(Q/A2))+1/2・ρ・A1・((Q/A2)2-(Q/A1)2)
=1/2・ρ・Q2・(A1-A2)2/(A1A22)
反力fxは上下一対の斜板から受けるものでありしたがって1枚あたりの反力成分Fxは
Fx=1/4・ρ・Q2・(A1-A2)2/(A1A22)
斜板に垂直な反力Fは
F・sinθ=Fx
一方
sinθ=1/2・(A1/B-A2/B)/L=1/2・(A1-A2)・B・L
よってFは
F=Fx/sinθ
F=1/2・Q2・B・L・(A1-A2)/(A1・A22)
以上(3-1)のように微小部分に作用する力を積分して求める方法に比べ現象解析作業や計算工数を少なくして
解を求めることができる。
以上
次回は捻り振動を伴う回転系の運動について記述する。