XCOMBの燃焼圧解析機能　　[XCOMB画面へ]

　−熱発生率のWiebe関数近似−

　1Dエンジンシミュレーションでは熱発生率を入力するタイプの燃焼モデルが多く用いられます.　熱発生率データは燃焼圧計測結果から得られたものをクランク角毎の表データとして

入力することもできますが熱発生パターンの変更に際し手間がかかるため近似式で与えた方が便利です.

過去の多くの研究からWiebeにより提案された指数関数がエンジンの熱発生率カーブを良く近似できることが知られており、したがって1Dシミュレーションコードの多くは下式に示す

Wiebe関数の形式で入力できるようになっています.　

dQ/dθ=Qf・a・(m+1)・θ^m/θ_b^m+1・e^{-a(θ/θb)^(m+1)}

dQ/dθ：単位クランク角当りの熱発生量(熱発生率)

Qｆ：燃料の全発生熱量

θ：燃焼開始点からの経過クランク角 θ=α-(θig+θd) α：クランク角

θd：着火遅れ

θig：点火時期

θ_b：燃焼期間

a、m：Wiebe関数における係数

　熱発生率のWiebe関数近似とは燃焼圧解析で得られた熱発生率カーブとWiebe関数で近似したカーブとの誤差を最小とするようa、m、θ_b、およびθdを決定することです.

XCOMBには独自の手法による熱発生率のWiebe関数による近似機能が備わっています.

--------------------------------------------------------------------------------------------------------------------------------

【解析条件】

＜エンジン＞

　　4サイクル ガソリン吸気管噴射エンジン

＜運転条件＞

　　1000rpm　スロットル部分開度　点火時期30degBTDC 空燃比14:1

＜燃焼圧解析結果として得られた熱発生率カーブ＞

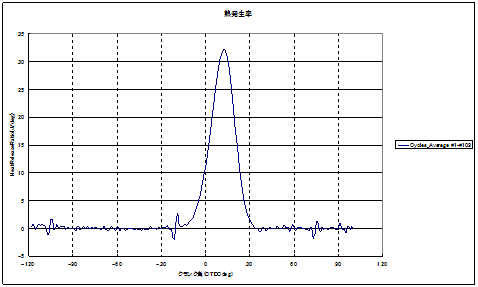
＜曲線近似（カーブフィッティング）の手法＞

熱発生率カーブの近似が目的なので実測の熱発生率カーブを目標として変数を最適化する熱発生率ベースのカーブフィットを行えばよいと考えられるかも知れませんが

実際の熱発生率演算は燃焼室壁への熱損失、ガス比熱、燃料蒸発熱など多くの熱力学的仮定に基いており、熱発生率ベースのカーブフィットを行った場合、

近似で得られた熱発生率を用いて計算した筒内圧が計測値と良い一致を示さないことがあります.

これに対し元々計測された量は筒内圧であることから、仮定した熱発生率カーブを用いてシミュレーション計算した筒内圧と計測された筒内圧との誤差が最小となるよう

カーブフィットを行う方が合理的であると考えられ、これを筒内圧ベースのカーブフィットと呼びます.　勿論筒内圧から熱発生率を求める演算と熱発生率から筒内圧を求める

演算とは共通の熱力学的仮定を用いた（相互）逆算関係にある必要があります.

XCOMBは筒内圧ベースと熱発生率ベースのカーブフィットを選択できますが、ここでは筒内圧ベースのカーブフィットについて解説します.

【解析結果】

＜Wiebe関数近似の設定＞

熱発生率計算結果が保存されているワークシートを元にWiebe関数近似を行う際の最適化変数、熱伝達率の近似式(EichelbergまたはWoschni)、および

Wiebe関数のタイプ(Single：ガソリンの場合　Double：ディーゼルの場合))を選択し近似を実行します. この時最適化変数にはデフォルト値が用いられます.

今回は４サイクルガソリンエンジンなので熱伝達率の近似式はWoschniを、Wiebe関数はSingleを選択します.

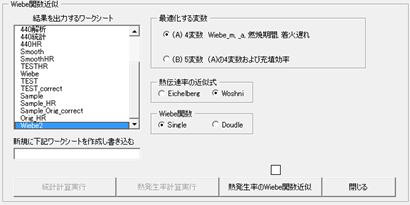　Wiebe近似の設定画面

　 デフォルト値

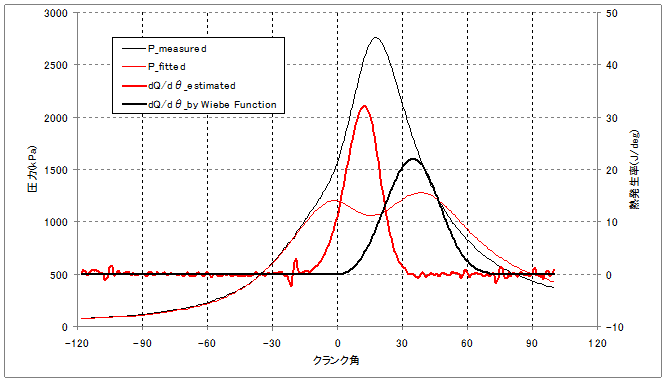
＜初期値での近似結果＞

熱発生率の計算（近似）結果は実測値と大きく異なっておりしたがって燃焼圧も計算と実測で大きく乖離しています.

＜変数の探索範囲＞

上表に示す初期値（デフォルト値）では良いカーブフィット解が得られなかったので４つの変数の解を以下の範囲内で探索します.

0≦Td≦30　　20≦Tb≦80　　1≦m≦4　　5≦a≦9

＜目的関数＞

目的関数Objectiveは筒内圧ベースの最適化ではクランク角αが吸気閉TICから排気開TEOの区間の筒内圧実測値P_measuredとシミュレーション計算（近似）値P_fittedとの

誤差の2乗和でありカーブフィッティングではObjectiveを最小化するよう変数を最適化します.

_TEO

Objective=Σ(P_measured – P_fitted)²

^α=TIC

＜Excelソルバを用いた探索＞

XCOMBではExceの標準アドインソフトである’ソルバ’を用いて最適化を実行します.

目的関数の入力された目的セルは$K$6、目標値は最小化、変数セルの範囲を$K$3:$N$3とし各変数の制約条件を上図のように入力したあとExcel2010では‘解決方法の選択’で

’エボルーショナリー’エンジンを選択して[解決]を実行します. このカーブフィット問題は非線形性が強いので探索範囲全域を隈なく探索するエボルーショナリーエンジンが適切ですが、

探索エンジンの選択機能のないExcel2003では続けて数回実行すればその度に解が改善されエボルーショナリーエンジンの解に近い解が得られることがあります.

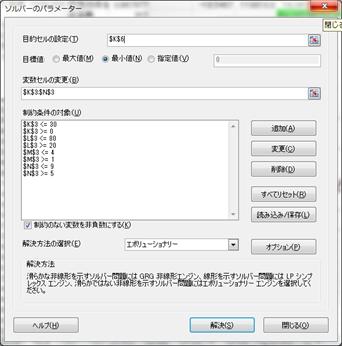Excel2010のソルバパラメータ設定画面

＜変数最適値＞

ソルバで得られたTd、Tb、m、a、夫々の解はワークシートのセルに表示されます.

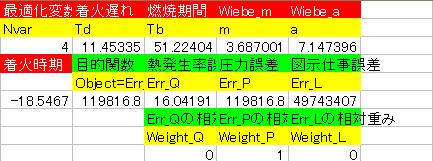　最適化結果表示

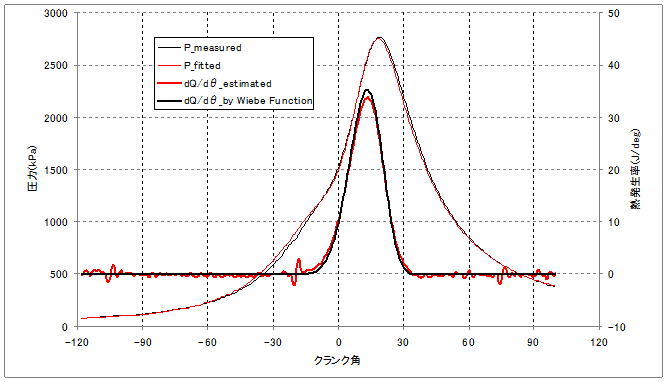
＜圧力および熱発生率カーブ＞

圧力、熱発生率とも良い近似ができていることが確認できます.

*****************************************************************************