極方程式と曲線

雛形を利用して、色々なグラフを描きます。

色々な極方程式のグラフを描く

"MyApp.h" で、曲線の定義域を (0, 20) へ変更します。

#include	<MyCurve.h>
#include	"MyCurve2.h"


class MyApp : public MyMainWnd{
public:
	// 曲線を描く
	void wmPaint(HDC hdc){
			// メモリデバイス
			MyMemoryDC mdc(hdc, 600, 400);
			MyDC g(mdc.hdc);
			
			// 座標変換
			g.Trans(50, 0, 0, -50, mdc.width / 2, mdc.height / 2);
			
	
			MyCurveX mcX;	// x軸
			MyCurveY mcY;	// y軸
			MyCurve2 mc;	// 曲線
			
			// 座標軸--------------------------------------------------------
			g.Pen.Color(0, 0, 255);	// 青色のペン
			// ｘ軸
			g.draw(mcX, -10, 10);
			// ｙ軸
			g.draw(mcY, -10, 10);
			
			// 曲線を描く
			g.Pen.Color(0, 0, 0);	// 黒色のペン
			g.Pen.Size(2);
			
			g.draw(mc, 0, 20);
			//=================================================================
			// スクリーン画面へコピー
			mdc.BitBlt(10, 10);
	}
};

極形式

極方程式は、r = f(Θ) で表される曲線です。 これを、

x = f(Θ)cosΘ
y = f(Θ)sinΘ

として曲線を描きます。

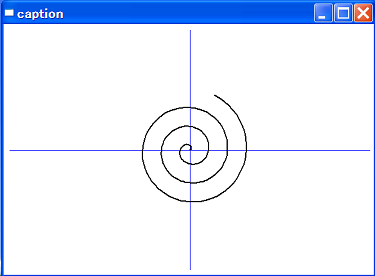
アルキメデスの渦巻き線（win223-1）

r = aΘ ですから、x = aΘcosΘ, y = aΘsinΘ となります。

// 曲線
class MyCurve2 : public MyCurve{
public:
	double a;
	
	double fx(double t){
		return a * t * cos(t);
	}
	
	double fy(double t){
		return a * t * sin(t);
	}
	
	MyCurve2(){
	 	a = 0.1;
	}
};

a = 0.1 としました。

実行画面です。

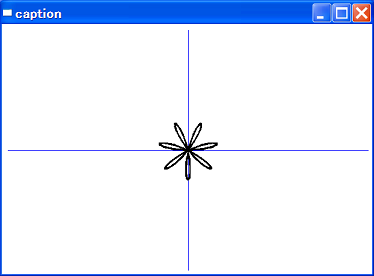
正葉線(win223-2)

r = sinaΘ で表される曲線を、正葉線といいます。

// 曲線
class MyCurve2 : public MyCurve{
public:
	double a;
	
	double fx(double t){
		return sin(a * t) * cos(t);
	}
	
	double fy(double t){
		return sin(a * t) * sin(t);
	}
	
	MyCurve2(){
	 	a = 7;
	}
};

実行画面です。

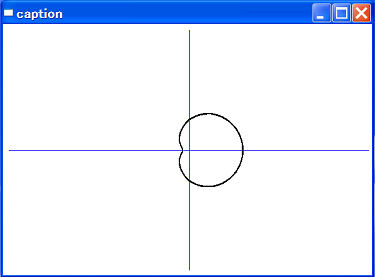
リマソン(win223-3)

r = a + b cosΘ で表される曲線を、リマソンといいます。

// 曲線
class MyCurve2 : public MyCurve{
public:
	double a, b;
	
	double fx(double t){
		return (a + b * cos(t)) * cos(t);
	}
	
	double fy(double t){
		return (a + b * cos(t)) * sin(t);
	}
	
	MyCurve2(){
	 	a = 1;
		b = 0.8;
	}
};

実行画面です。

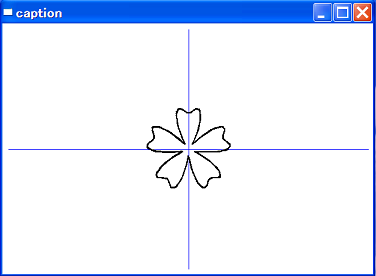
花びらの形(win223-4)

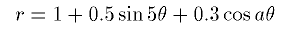
// 曲線
class MyCurve2 : public MyCurve{
public:
	double a;
	
	double fx(double t){
		return (1 + 0.5 * sin(5 * t) + 0.3 * cos(a * t)) * cos(t);
	}
	
	double fy(double t){
		return (1 + 0.5 * sin(5 * t) + 0.3 * cos(a * t)) * sin(t);
	}
	
	MyCurve2(){
	 	a = 10;
	}
};

---

[前] [目次]