時計

時計の針

時計の針について考えます。

TestMyTokei02.java

import java.awt.Color;
import java.awt.Graphics2D;

import myMath.Tpl10;

public class TestMyTokei02 extends Tpl10 {

	int t = 0;

	public void init() {
		tr.move(getWidth() / 2, getHeight() / 2);
		tr.set(1, 0, 0, -1);
		tr.scale(50);
		setTimer(10);
	}

	public void draw(Graphics2D g2) {
		// ｘ軸、ｙ軸
		g2.setColor(Color.black);
		g2.draw(tr.LineX());
		g2.draw(tr.LineY());

		double x, y;

		x = Math.cos(Math.toRadians(t));
		y = Math.sin(Math.toRadians(t));

		g2.draw(tr.Line(0, 0, x, y));
		t++;
	}
}

解説

原点を中心とし、半径 \( r \) の円上の点の座標は、\( x \)軸からの回転角を \( \theta \) とすると、次の式で与えられます。

\[ \begin{cases} x = r \cos \theta \\ y = r \sin \theta \end{cases} \]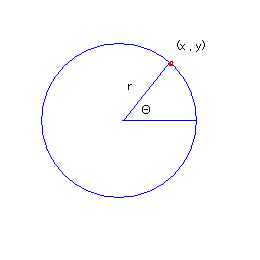

\( \theta \) を \( \cfrac{1}{10} \) 秒に１°増やしていくと点が回転します。 この点と原点を結べば時計の針となります。

---

[前へ] [戻る] [次へ]